-

Gravitational Waves: Memory, Symmetries and Charges
Gravitational wave memory is the residual stretching and squeezing of spacetime due to the passage of a gravitational wave arising from, for example, the merger of black holes. This fundamental property of gravitational waves is deeply related to the underlying (asymptotic) symmetries of spacetime, the existence of infinitely many “conserved” charges in classical scattering and has been argued to play a significant role in flat space holography and the black hole information paradox.
C.Ferko, G. S. and S. Sethi, “Gravitational Memory and Compact Extra Dimensions”, Phys. Rev. D 105, 024072 (2021). arXiv: 2109.11599
G.S. and R. M. Wald, “The Asymptotic Behavior of Massless Fields and the Memory Effect”, Phys. Rev. D. 99 084007 (2019). arXiv: 1901:05942
G. S. and R.M. Wald, “Memory Effect for Particle Scattering in Odd Spacetime Dimensions”, Phys. Rev. D 97 2 024036 (2018). arXiv: 1712.00873
-

Scattering Theory in Quantum Field Theory and Quantum Gravity
A major tool of quantum field theory (QFT) is the “S-matrix” which describes the evolution of quantum fields from asymptotically early to late times. Despite the utility of this approach, the S-matrix is only well-defined for the scattering of massive fields. For the scattering of massless fields (i.e. EM and gravitational fields) the standard S-matrix is infrared-divergent. A complete description of scattering theory is necessary for describing, for example, the information content of low frequency radiation and black hole evaporation in asymptotically flat spacetimes.
K. Prabhu, G. S. , R. M. Wald, “Infrared Finite Scattering Theory in Quantum Field Theory and Quantum Gravity” Phys. Rev. D 106, 066005 (2022). arXiv:2203.14334
K. Prabhu & G. S. “Infrared finite scattering theory: Scattering states and representations of the BMS group” arXiv:2203.14334
K. Prabhu & G. S. “Infrared finite scattering theory: Amplitudes and soft theorems” arXiv:2402.18637
-

Quantum Superpositions and Observational Quantum Gravity: Entanglement and Decoherence
A fundamental theory of quantum gravity remains the most significant open issue in theoretical physics. To bridge this gap, tabletop experiments have been recently proposed to study quantum superpositions of massive objects. Such experiments hope to directly probe the quantum nature of gravity by measuring entanglement and decoherence mediated by the gravitational field. It is essential to determine which aspects of quantum gravity are accessible to such experiments and if such (gedanken)experiments can provide insight into the nature of quantum gravity.
D. Danielson, G. S. , R. M. Wald, “Gravitationally Mediated Entanglement: Gravitons vs. the Newtonian Field” Phys. Rev. D 105, 086001 (2022). arXiv: 2112.10798
D. Danielson, G. S. , R. M. Wald, “Black Holes Decohere Quantum Superpositions” Third prize essay in the Gravity Research Foundation 2022 Essays on Gravitation. Int. J. Mod. Phys. D 2241003 (2022). arXiv:2205.06279
D. Danielson, G. S. , R. M. Wald, “Killing Horizons Decohere Quantum Superpositions” arXiv: 2301.00026
Click here for a list of talks
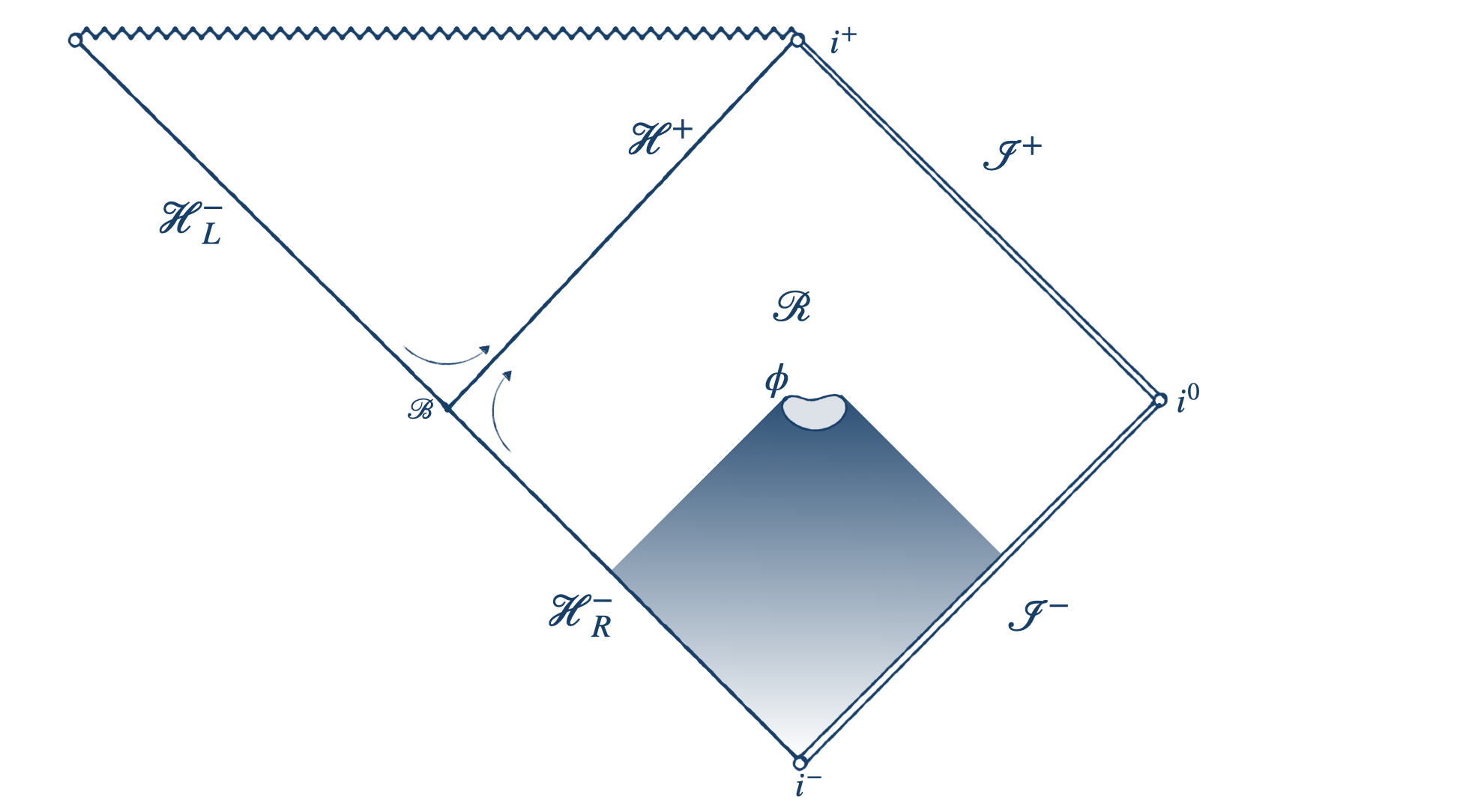
Generalized Black Hole Entropy is von Neumann Entropy
We show that the von Neumann entropy of physical “gravitationally dressed” observables in the exterior of any black hole is equivalent to the generalized black hole entropy.

Black Holes Will Eventually Destroy All Quantum States, Researchers Argue
Quanta article by Thomas Lewton on our recent series of papers on horizons “observing” quantum superpositions. Image by Kristina Armitage.
Other articles written about this work:
Researchers Argue Black Holes Will Destroy All Quantum States - Thomas Lewton (Wired)
Black holes destroy nearby quantum superpositions, thought experiment reveals - Jacklin Kwan (Physics World)
Black holes resolve paradoxes by destroying quantum states - Lisa Grossman (Science News)
Researchers Argue Black Holes Will Destroy All Quantum States (Wired)
Extreme Horizons in Space Could Lure Quantum States Into Reality - Mike Mcrae (Science Alert)

Killing Horizons Decohere Quantum Superpositions
We recently showed that the mere presence of a black hole will eventually decohere any superposition in its exterior. We now show that, more generally, decoherence of stationary superpositions will occur in any spacetime with a Killing horizon. This occurs because, in effect, the long-range field of the body is registered on the Killing horizon which, we show, necessitates a flux of "soft horizon gravitons/photons" through the horizon. The Killing horizon thereby harvests "which path" information of quantum superpositions and will decohere any quantum superposition in a finite time. We particularly analyze the case of a uniformly accelerating superposition in flat spacetime which, from the Rindler perspective, is decohered due “soft” Rindler gravitons/photons which, from the inertial perspective are “hard” inertial gravitons/photons at null infinity. We also analyze decoherence due to the presence of the cosmological horizon in de Sitter spacetime. We provide estimates of the decoherence time for such quantum superpositions in both the Rindler and cosmological cases.
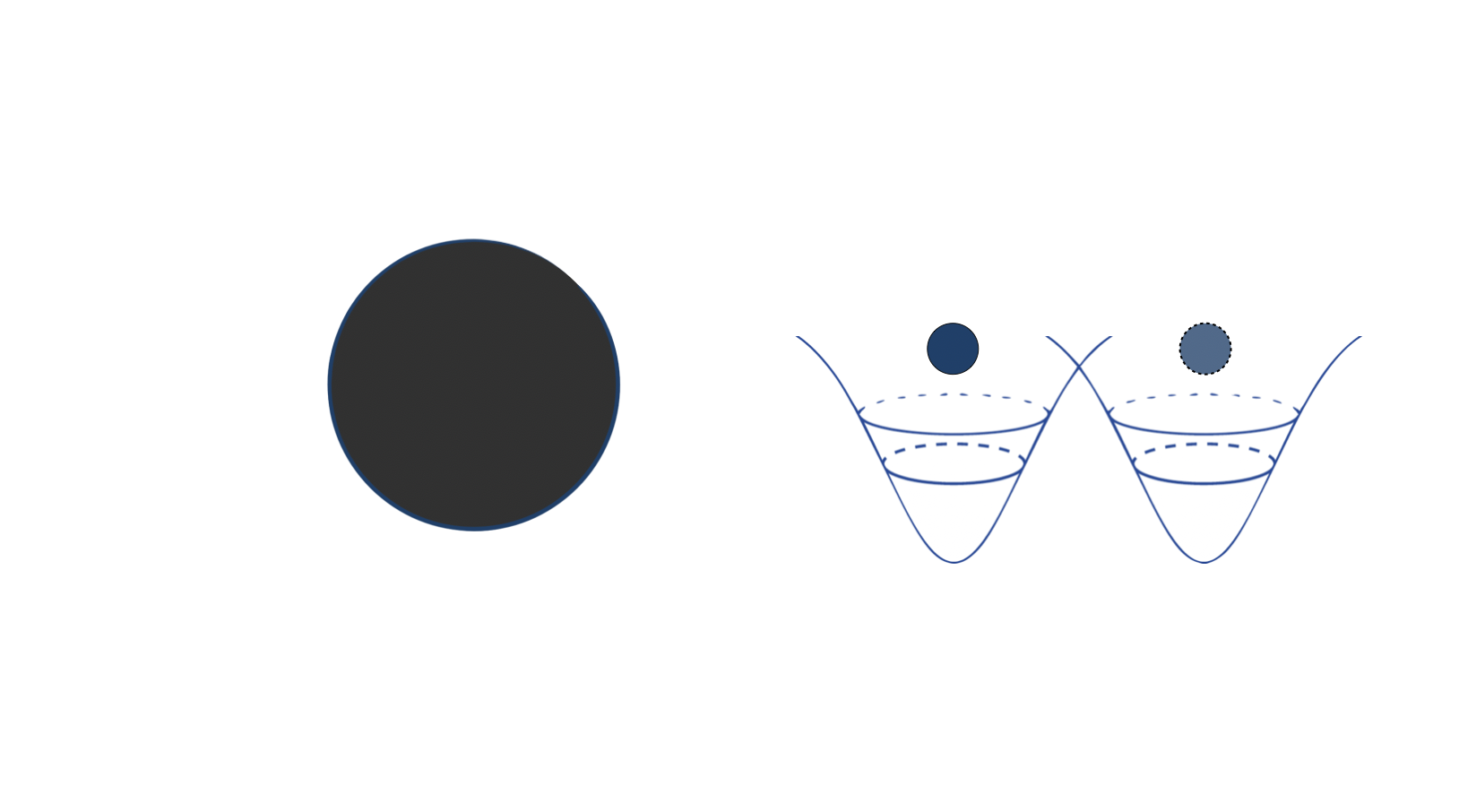
Black Holes Decohere Quantum Superpositions
We show that if a massive body is put in a quantum superposition of spatially separated states, the mere presence of a black hole in the vicinity of the body will eventually destroy the coherence of the superposition. This occurs because, in effect, the gravitational field of the body radiates soft gravitons into the black hole, allowing the black hole to acquire "which path" information about the superposition. A similar effect occurs for quantum superpositions of electrically charged bodies. We provide estimates of the decoherence time for such quantum superpositions. We believe that the fact that a black hole will eventually decohere any quantum superposition may be of fundamental significance for our understanding of the nature of black holes in a quantum theory of gravity.

Infrared Finite Scattering Theory in Quantum Field Theory and Quantum Gravity
We prove that there is no preferred Hilbert space for an (infrared-finite) scattering in general QFTs and quantum gravity. The procedure that works in massive QED fails in all other theories and we argue that there are no other alternative constructions. Therefore we advocate that scattering theory, at a fundamental level, should be formulated algebraically where “in” and “out” states are simply defined as lists of correlation functions without any reference to a preferred Hilbert space!

Gravitationally Mediated Entanglement: Newtonian Field vs. Gravitons
A fundamental theory of quantum gravity is the “holy grail” of physics. However, due to the lack of experiments, there is no agreed-upon formulation of this theory. As noted by Richard Feynman in the 1950’s, one can attempt to gain insight into quantum gravity by considering the gravitational effects of quantum superpositions. Remarkably, such superpositions are within range of being created experimentally! This paves the way for a new era in tabletop experiments in quantum gravity.
In this article, we precisley analyze what these experiments can teach us about the quantum nature of gravity. By rigorously studying a gedankenexperiment involving the superposition of massive bodies we argue that entanglement generated by the Newtonian gravitational field cannot be locally distinguished from entanglement via gravitons (the fundamental particle of gravity). Therefore, the experimental verification of Newtonian entanglement implies the existence of the graviton.
Coauthors: Robert. M. Wald and Daine. L. Danielson
ArXiv: 2112.10798 [quant-ph]

Gravitational Memory and Compact Extra Dimensions
The most robust prediction of string theory is the existence of extra dimensions. The fluctuations of these extra dimensions produce, in addition to gravitational and EM degrees of freedom, a set of scalar fields (i.e. the “moduli space”) whose masses can be (potentially) very light. It is extremely important to find observables sensitive to the presence of light scalars and, if such scalars come from dimensional reduction, use these observables to determine the structure of the compact space.
In this paper we study gravitational radiation with arbitrary compact “extra dimensions” (i.e. any Ricci-flat Riemannian manifold). We determine the nonperturbative, gauge invariant radiative observables and apply this formalism to spacetimes which contain a burst of radiation. We llustrate how the fluctuations of the compact dimension provide an “effective energy flux” which influences a gravitational wave detector and encodes the structure of the compact space. This provides a precise way of using gravitational waves to probe the “internal space”.
Coauthors: Savdeep Sethi and Christian Ferko
ArXiv: 2109.11599 [gr-qc]
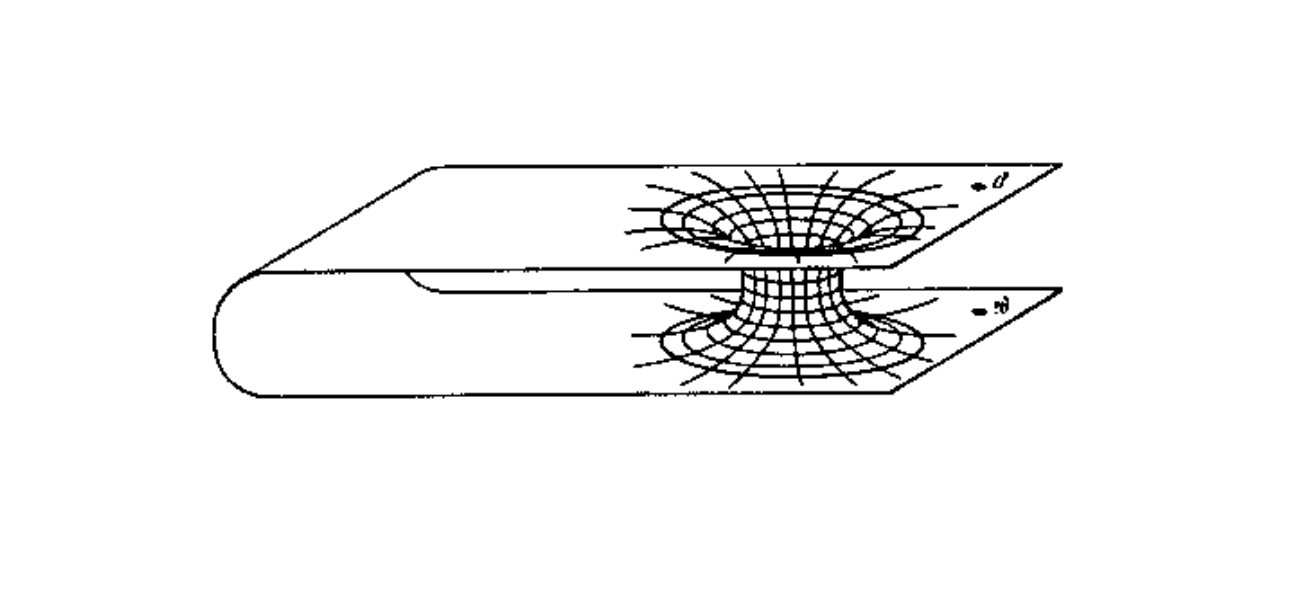
Blázquez-Salcedo-Knoll-Radu Wormholes Are Not Solutions to the Einstein-Dirac-Maxwell Equations
Macroscopic, traversable wormholes are hard to make! It is well known now that such traversable wormholes require the presence of “negative energy” matter. In a recent letter, the authors claimed to circumvent these issues and construct a genuine traversable wormhole using Dirac fields (i.e. the field of the electron).
In this paper, we prove that their wormholes are in fact not solutions to the Einstein-Maxwell-Dirac equations.
Coauthors: Robert M. Wald, Robert J. Weinbaum and Daine L. Danielson
ArXiv: 2108.13361 [gr-qc]
Daine L. Danielson, G. S., Robert M. Wald, and Robert J. Weinbaum, Phys. Rev. D 104, 124055
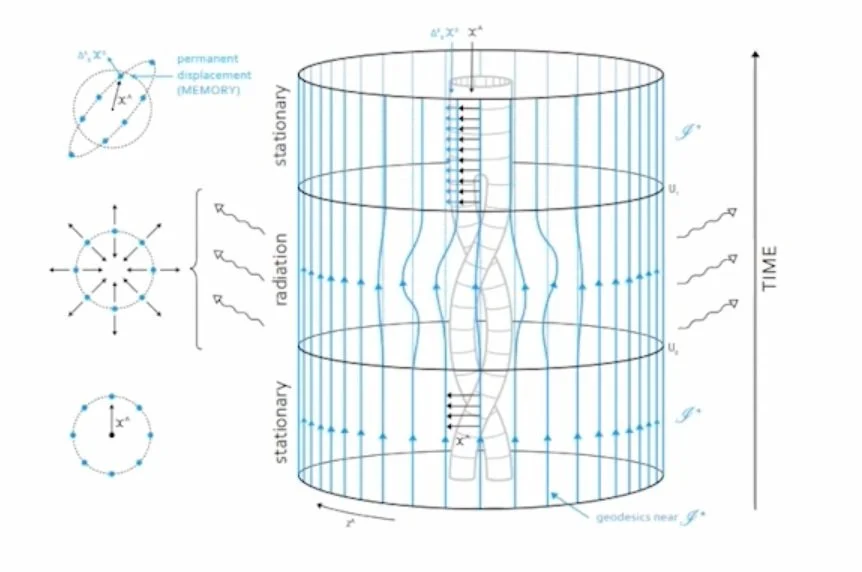
The Asymptotic Behavior of Massless Fields and the Memory Effect
In 2016, Stephen Hawking, Malcolm Perry and Andrew Strominger (HPS) wrote a fascinating paper linking ideas regarding the “gravitational memory effect” (a classical effect of gravitational waves detectable by LIGO or LISA), the “asymptotic symmetry group” (the infinite set of “BMS“ symmetries of asymptotically flat spacetimes) and infrared divergences in quantum gravity (divergences in scattering amplitudes due to the emission of low-frequency gravitons). The connection between these three ideas has been argued to play a significant role in the black hole information paradox.
In this (long!) paper we systematically analyze the connections between these three ideas in four and higher dimensions. Along the way, we rigorously analyze gravitational waves in all dimensions, generalize the notion of the memory effect, discover new memory effects in all dimensions (including four) and clarify the link between memory, asymptotic symmetries and IR divergences. In totality, we conclude that the fascinating connections between these three ideas are really special to four dimensions.
Coauthors: Robert M. Wald
Arxiv: 1901.05942 [gr-qc]
Cosmography of KNdS Black Holes and Isentropic Phase Transitions
Coauthors: J. McInerney and J. Traschen
arXiv: 1509.02343 [hep-th]
Gravitational Memory image credit: Stefan Hollands, Quantum Superposition image credit: Figure 3 in paper by D. Carney, P. C. E. Stamp and J. M. Taylor